Always Noticing and Wondering

Last Thursday started out like so many have in the last 20+ years.  I logged into our Problems of the Week site, preparing to read through the student submissions to one of our Current PoWs so that I could choose some to include with the commentary I write. Last week I was doing the Geometry Problem of the Week. And as has happened on almost every “Geometry Thursday” in the last 20+ years, I saw this name in the group of people who were the first people to look at the problem when it was available on our site:

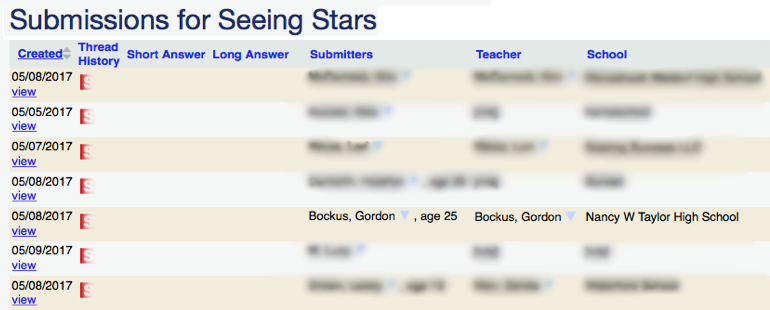
Gordon has been using our Problems of the Week for many years. Here’s a snippet from an email he sent me in November of 2010:

Hi, Annie. I am still teaching here in Oklahoma. I just thought I would touch base. […] How are things with you? It has been a while since Swarthmore and only the Geometry PoW.

A while, indeed!  We started the Geometry PoW in 1993, and added the Elementary PoW (since renamed the Math Fundamentals PoW) a couple of years later. In November 2014 Gordon wrote:

Somewhere there is probably a picture of Gordon and me from that San Diego meeting. I did find two pictures of us from subsequent NCTM Annual Meetings.

(Yes, in the San Francisco picture I am dressed as an anonymous superhero. Ask me about it sometime.)

Gordon hasn’t had many students submit to our problems online, but for many years, he has had a bulletin board outside his classroom where students could get the problems and then give a solution to him for extra credit.  The only students of his who consistently submitted online were his three children. Oldest child Gordon Jr. started submitting in 1996 when he was a senior in high school (and continued during his first year of college). Middle child Mike started in 1998, and youngest Regina started in 2005.

In the spring of Gordon Jr.’s senior year of high school, we used a question about how to make a hexagonal cross section of the cube. In my commentary about the solutions we received, I wrote, “There were some innovative methods used to find the hexagon. Berno W. says he used a potato. Gordon Bockus went out to the woodshop and built the figure.”  The next April, at the NCTM Annual Meeting in Washington, D.C., Gordon Sr. stopped by our booth in the exhibit hall and said, “I have something for you. Gordon Jr. wanted me to give you this.”  Out of his bag, he pulled Gordon Jr.’s sliced cube! As you can see, he had written on it, “I know it’s not regular, but it pointed me in the right direction. Gordon Bockus Jr.”  It has lived on my desk every since.

Gordon would occasionally submit his own solutions to problems, telling me why he liked them, describing how he was going to use them with his students, or asking a question about a problem or its extra question.  His bulletin board persisted.  In his November 2010 email, he told me how his two boys (by then both married with kids) were doing, and said, “Whenever one of them visits me at school, they see the PoWs up on the bulletin board and they ask if Annie is still involved.” In that email he also mentioned retirement, but added, “I don’t know when that will happen. I don’t know what I would do in place of teaching.”

In November of 2014 he wrote, “Retirement is on my mind but I don’t think I can go quietly. So I might be around another year.”  Well, here we are, three years later, and Gordon is in fact retiring at the end of this school year.  And he’s going out with a bang, as his Academic Team won the Oklahoma State Championship in February and Gordon was named Oklahoma Academic Competition Association Coach of the Year for the second time (he also helped start academic bowl competitions in Oklahoma).

This means that starting this fall, I’ll no longer see Gordon’s name at the top of the submission queue on Thursdays, and I’ll miss that reminder of our long friendship and his years as a devoted Problem of the Week user.  However, as I wrote in email to Gordon last spring, Gordon Jr.’s sliced cube will always have a prominent place on my desk.  It represents the great connections that I’ve made throughout the years with Gordon and his children, as well as many other students and teachers, and also ways in which students explore math that go above and beyond what we might expect.

Thank you, Gordon, for being a member of our community for so many years and for sharing your love of mathematics with so many students. Enjoy retirement!

May the 4th was not only Star Wars Day but was also my mother’s birthday. She died in February 2014.  I decided to celebrate by taking a vacation day and digging in the garden, which was one of my mother’s favorite things to do (I’m pretty good in the garden, but I swear she could weed at least four times faster than me, and yes, I totally took advantage of that by enlisting her help more than once!).  I did some weeding, including the final cleaning out of this one area of the yard into which we are transplanting a bunch of irises and day lilies that our neighbor was removing from his front yard (our new neighbors are not plant fans, apparently – they have also cut down a dogwood and a Japanese maple).

When loosening the soil in the bed, I hit a rock, and decided that I’d dig it up (another thing my tenacious and hard-working mother would have done).  It turned out to be two large rocks – the one in the picture that includes my foot for scale (Estimation180 anyone?) and the one leaning against the fence in the other picture (which includes a pint glass for scale).

But enough about my day off. This is a math blog, after all, so I really wanted to talk about how my mother not only persevered when faced with a giant rock in her flower bed, but also when she was designing some of her fabulous textiles.  Let’s start by watching the Ignite that I did about her at NCSM last spring, shortly after she died.

She’s pretty talented, huh?  For fun, and to further honor her talents on her birthday, I decided to try to reproduce that Celtic design that she found in a book. As you may recall from the video, here’s the picture that she had to work with:

I stared at it a bit and thought about what I would need to pay attention to if I was going to reproduce it using Geometer’s Sketchpad (that is another way of saying that I Noticed and Wondered).  Yes, Mom worked on paper, and didn’t have any problem redoing things as often as necessary, but I believe in the power and speed of something like a dynamic geometry environment so that the tweaking goes a lot faster once you’ve set up the initial relationships!

As shown below, I took note of several things.  First, the whole thing is a circle[1].  Second, there are 12 outer points (marked in red).  There are also 7 concentric circles underlying the design (marked in blue).  I noticed that I would need to construct 24 radii of the outer circle, and create points of intersection where those radii crossed the concentric circles.  I also noticed that one “path” through the design consisted of “diagonals” of the spaces created by these radii and circles (marked in green).

In Picture 1 below, I’ve set up the initial relationships noted above.  In Picture 2 I’ve rotated that one path 11 times by 30 degrees, resulting in the beginning appearance of those 12 outer points.  In Picture 3, I’ve added the “paths” going the other way. (Yes, I rotated – leveraging symmetry and using transformations in Sketchpad.  In fact, I made custom transformations that rotated by 15 and 30 degrees that I could apply to any object I constructed to save a lot of time.)

It’s really starting to look like something!  I can use the points along the thick radius to change the size of the circles and, consequently, the shape of the paths.  One of my mom’s first sketches was a bit too “pointy”, and I’ve replicated that by making every circle but the outer one a lot smaller.  (You may be able to see a couple of the circles that she drew and then erased.)

I was able to drag the points that control my circles until I got it just the way I wanted it.  I didn’t see any more trial sketches in my mother’s files, but I do know that she definitely nailed it in the end!

Consider all the sense-making she did.  She couldn’t just measure the picture, since it was drawn in perspective, but she took away as much information as she could.  She noticed relationships and used trial and error to figure out the parts she couldn’t count.  She made mistakes and learned from them.  And there is no question that she persevered!

As I said in my Ignite talk, we need to be sure to look for and value these traits in our mathematicians, not just their ability to crank out answers to a lot of textbook problems really quickly.  Look for opportunities for your students to practice sense making, maybe even by having them replicate some drawings!

I’ll close with one more picture of my mom’s artwork taken in 2008.  She made this quilt of the Math Forum’s dragon fractal logo for us to hang in the office.  Did she know what a dragon fractal is?  Nope.  But she had the ability to pay attention to detail enough to get it right nonetheless.  Also in the picture is my husband Riz (the tall one – Estimation180 clue is that I’m 5’10”), my sister Marty, her husband Silas, and their adorable children Olivia (7), Liam (4), and Clare (8 months).

My mother inspired me in many ways as an artist and as a mathematician.  We should all try to do the same for the young people in our lives.

[1] As my friend and math teacher/former architect Peg Cagle pointed out after I wrote this, it’s not a circle at all!  Read more about the Piazza del Campidoglio or look for pictures yourself. 

[originally posted to my now-defunct blog at The Math Forum]

Before you read anything else, go play Game About Squares.  Seriously.  Don’t come back here until you’ve gotten to Level 8.  But do come back – don’t let it suck you in permanently!

(Did you really go play?  Honest?  Because if you didn’t, the latter part of this post won’t be as much fun to read.)

Last month we were in Boston for the NCSM and NCTM yearly meetings, and as has recently happened at large math ed events, I was occasionally hailed with some version of, “We just used your video in our talk!” or even “OMG!  We use your video in ALL of our PD! You’re famous in [insert state, county, or district here]!  Can we take our picture with you??”  Invariably, they’re referring to the very first Ignite talk I gave, which was at NCTM in Indianapolis in 2011 (though it wasn’t technically part of NCTM, since the session didn’t get accepted, so we did it in a bar).  If you haven’t seen it, or haven’t watched it lately, I encourage you to check it out.

Many groups are using this video as a launch for professional development because it can start conversations about moving beyond answer-getting and instead valuing as many of students’ mathematical ideas as possible.  As of this writing, the video has been viewed over 15,800 times.  That’s really exciting!  And I certainly don’t mind being stalked at math ed conferences.

This past year I wrote math curriculum, mentored college students doing academic tutoring, and did some tutoring myself for a group of high school sophomores from under-resourced schools participating in Project Blueprints, an after school youth empowerment program hosted by Swarthmore College. One thing we focused on early in the year was developing and emphasizing mathematical habits of mind and working towards getting the students to believe that they have mathematical ideas and that those ideas are important.  We did a lot of Noticing and Wondering!  In fact, one of the first activities we did when they got the new iPads was to play Game About Squares.

Now, these are kids who are taking high school geometry and are about to take the state’s Algebra exam for a second time (their district doesn’t have a very high success rate – one kid claimed that nobody from their district has ever passed).  Isn’t this supposed to be math support?  Do they really need to play a game?

Well, yes.  Students opened the game and were confronted (as were you, if you followed my directions to play before reading) with this:

“What are we supposed to do?”

“How does it work?”

“Where are the directions?”

“Uh….”

Those were a few of the comments I heard from the two pairs of students I was working with that day (and the one other adult in the room, who had pulled out her phone to try playing).  I just said, “Figure it out.”

Not surprisingly, they did.  They noticed, they wondered, they tried things, they guessed and checked, they made mistakes, they groaned, they backtracked, they started over, they laughed, they talked to each other a lot, they persevered, and they were excited by and proud of their progress.  What teacher wouldn’t want those things to happen in their math classroom on a regular basis?

An especially fun moment happened when Ashley, one of the coordinators of the program, came into our room.  She asked what they were doing and one of the students reset the game to Level 0, handed the iPad to her, and said, “Here.”

She asked, “What am I supposed to do?”, and the students just grinned and wouldn’t say a word.  I gave her a “don’t look at me!” shrug.  They watched Ashley’s finger hover over the screen to see what she would click on.  They snuck glances at her face to see if they could tell how she was feeling.  They grinned some more.  They elbowed each other gently when she made the same mistakes they had made.  They watched her slowly figure out how the game worked.  It was almost magical to observe them watching an adult go through the same learning and figuring out process that they had just gone through.  They seemed almost entranced!

Then we talked about the game for a bit, and discussed the “habits of mind” they had employed to figure out the game – noticing and wondering, guessing and checking, persevering, struggling productively, learning from mistakes without worrying about making mistakes (since they knew the only way they were going to make progress was to make mistakes and learn from them), and working together.  We talked about how these skills are as important as any content they learn in their school classes, and how they can use those skills to make progress on math problems they’re not sure how to solve.  In fact, much of the math programming we did the rest of the year employed huge doses of Noticing and Wondering and generating ideas about math situations, or scenarios (a math problem with no stated question).  Anecdotal reports suggest that by the end of the year, most of the students felt pretty confident that they could generate ideas about most math situations we handed them.  Big win!

These days we talk a lot about the importance of implementing and practicing the Standards of Mathematical Practice in classrooms.  Sometimes it’s hard to make that practice explicit, but students do need to know when they’re developing and using (and getting better at) those habits.  One way to do this is to do activities, such as Game About Squares, where there isn’t any real math “content”, but there is a lot to mess around with and figure out and enough support that students can do that without a lot of guidance from any adults.

I’d love to hear about your favorite such activities, and what sorts of subsequent conversations you have with your students about habits of mind.

Now go play Game About Squares some more.  After a hiatus, I’m currently working on Level 19, so I’ve got a lot of things to figure out!

[originally posted to my now-defunct blog at The Math Forum]

For a number of years, Max and I have done math methods workshops for the Swarthmore College pre-service teachers, usually on Sunday afternoons.  At the end of September we did two two-hour workshops for the elementary student teachers.  The first focused on encouraging and cultivating sense-making, and we modeled and discussed the Math Forum’s “I Notice, I Wonder” activity.  We knew from past years that this activity often gets a lot of traction, as the student teachers not only start trying it in their classrooms, but also end up finding themselves using it.  One member of the education faculty reported that everyone in her student teacher seminar was using it, not just the elementary and secondary math folks!

This year, the day after our first workshop, I received mail from Brooke, one of the student teachers.  She is student teaching in a 5th grade classroom in the district where I live.  (You might recall that my friend Debbie, who authored the last post on my blog, also teaches at an elementary school in the district where I live, and this year is teaching a section of 5th grade math, but she’s not at the same school as Brooke.)

Brooke was wondering if she could do I Notice, I Wonder with her students, even though she’d never done it before.  Short answer:  Absolutely!  For the longer answer, here’s the exchange that we had over the course of a couple of days.

(Note:  Brooke mentions “bar models” in her post.  For more info about that, check out this post from Erie 2 Math.  Some of you might know them as part-part-whole diagrams.)

So there you have it – the experience of a “first-timer”, captured in a few snippets.  I was excited that she thought to try it, very excited that she did try it, and super excited that she noticed the type of mathematical talk that it encouraged in the classroom and how it is serving as a foundation for sense-making for her students.

My colleague Max recently blogged about noticing and wondering in high school,  Noticing and Wondering in High School and I thought it would be fun to blog about using it at the elementary level.  The essence of our “I Notice, I Wonder” activity is that you give students a mathematical situation or picture or story, without asking any specific questions, and ask them to list everything that they notice about it, and everything that it makes them wonder about.

I’ve written about it in the past, including in one of our Teaching with the Problems of the Week documents, How to Start Problem Solving in Your Classroom [PDF].  In that, I tell the story of the first time I explicitly asked students (who were “low-level” eighth graders) to tell me everything they “noticed” about a picture.  The short version is that the students were awesome and their teacher was amazed at how much math they came up with.

Just as I started composing my post, I got email from my friend Debbie, who teaches at an elementary school school in the district I live in.  She described the first lesson she did with a new class she’s co-teaching, in which she asked the students to notice and wonder.  I asked her if I could use her story as a “guest post” on my blog, since I think it’s as compelling as anything I could have written.  She agreed, so here goes.